Complete question:
Two identical closely spaced circular disks form a parallel-plate capacitor. Transferring 2.1 × 10⁹ electrons from one disk to the other causes the electric field strength between them to be 1.6 × 10⁵ N/C . What are the diameters of the disks ?
Answer:
The diameter of the disks is 0.0174 m
Step-by-step explanation:
Given;
charge, q on each sphere = 2.1 × 10⁹ x 1.6 x 10⁻¹⁹ C = 3.36 x 10⁻¹⁰ C
Electric field strength due to charged spheres, E = 1.6 × 10⁵ N/C
E = V/d
Capacitance is given as;
C = εA/d
The charge on a capacitor is given as;
Q = CV
Q =
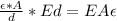
But, A = πd²/4
Q = E(πd²/4)ε
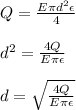
where;
d is the diameter of the disks
ε is permittivity of free space = 8.854 x 10⁻¹² F/m
Substitute the given values and solve for "d"

Therefore, the diameter of the disks is 0.0174 m