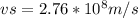Question

The ultraviolet Lyman alpha line of hydrogen with wavelength 121.5 nm is emitted by an astronomical object. An observer on Earth measured the wavelength of the light received from the object to be 607.5 nm. The observer can conclude that the object is moving with a radial velocity of

Answer 1

the observer can conclude that the object is moving with a radial velocity of
`vs = 2.76 * 10^8 m/s`

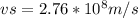
Step-by-step explanation:

In relation to Doppler effect for light, the formula can be represented as:

`\lambda = \frac {\lambda_0√((1 - \beta))} { √((1 + \beta))}`

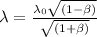
where,

`\lambda` = wavelength of the light emitted by an object = 607.5 nm

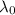`\lambda_0` = wavelength of ultraviolet Lyman-alpha line of hydrogen by astronomical object = 121.5 nm

`\beta` =
`\frac { vs }{c}`

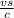
It is clear that the 'positive sign usually denotes "approaching" and the 'negative sign usually denotes "receding".

However, Since the object and the source are receding. Then, we have :

`\lambda = \frac {\lambda_0 (1 + \beta)^(1/2)}{ (1 - \beta)^(1/2)}`

`\frac {\lambda }{ \lambda_0} = ((1 + \beta)^1/2 )/(1 - \beta^1/2)`

`\frac {607.5 \ nm }{ 121.5 \ nm} = ((1 + \beta)^1/2 )/(1 - \beta^1/2)`

`5 = ((1 + \beta)^1/2 )/(1 - \beta^1/2)`

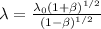
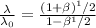
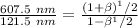
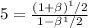
Squaring on both sides & we have:

`25 = (1 + \beta )/(1 - \beta)`

`25*{(1 - \beta)} = {1 + \beta }`

`25- 25 \beta = {1 + \beta }`

`- 25 \beta - \beta = 1 -25`

`- 26 \beta = -24`

`\beta = ( -24)/(- 26 )`

`\beta = ( 12)/(13 )`

`(vs)/(c) = ( 12)/(13 )`

`(vs)/(c) = 0.9231`

`{vs} = 0.9231 *{c}`

`{vs} = 0.9231 * 3*10^8 \ m/s`

`{vs} = 276930000`

`vs = 2.76 * 10^8 m/s`

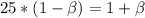
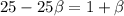
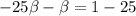
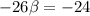
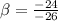
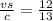
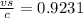
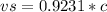
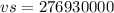
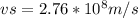
Therefore; the observer can conclude that the object is moving with a radial velocity of
`vs = 2.76 * 10^8 m/s`