Question

A long solenoid with 9.98 turns/cm and a radius of 6.52 cm carries a current of 24.8 mA. A current of 10.4 A exists in a straight conductor located along the central axis of the solenoid. (a) At what radial distance from the axis in centimeters will the direction of the resulting magnetic field be at 53.9° to the axial direction? (b) What is the magnitude of the magnetic field there?

Answer 1

a) 4.88 cm

b)
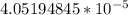`4.05194845*10^{-5` T

Step-by-step explanation:

The magnetic filed B inside the solenoid can be given as:

`B = \mu_onl`

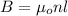
where

n = number of turns per meter = 9.98 turns /cm = 998 m⁻¹

`\mu_o` =
`4 \pi*10^(-7) N/A^2`

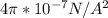
l = 24.8 mA = 0.0248 A

`B_(solenoid) = \mu_onl`

=
`(4 \pi*10^(-7) N/A^2)(998 \ m^(-1))(0.0248 \ A)`

=
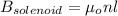
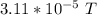`3.11 * 10^(-5) \ T` directed toward the axis

Now; the magnetic filed B from the wire is given by the formula;

`B = (\mu_oI)/(2 \pi s)`

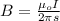
where;

s = distance of the wire

Thus; the magnetic field will be directed radially around the wire , therefore perpendicular as well to the solenoid axis

However; for the field to have an angle of 53.9° ; we have:

`tan ( (B_(wire))/(B_(solenoid) )) = tan \ 53.9^0`

`(B_(wire))/(B_(solenoid) ) =1.3713`

`B_(wire) =1.3713 *3.11*10^(-5)`

`B_(wire) =4.265*10^(-5) \ T`

`s = (\mu_ol)/(2 \pi B)`

`s = (4 \pi *10^(-7) N/A)^2*10.4)/(2 \pi * 4.265*10^(-5)T)`

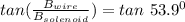
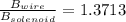
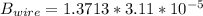
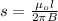
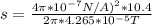
s = 0.0488 m

s = 4.88 cm

b)

What is the magnitude of the magnetic field there?

the magnitude of the field, is just the square root of the sum of the squares of
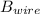`B_{wire` and
`B_{solenoid`

`\left(2.722\cdot10^(-5)\ +3.0015\cdot10^(-5)\right)^(2)\ -\ 2\left(2.722\cdot10^(-5)\cdot3.0015\cdot10^(-5)\right)`

=
`1.64182862*10^(-9)`

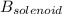
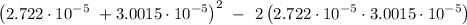
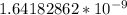
The square root of the answer =

`\sqrt{1.64182862*10^(-9)}`

=
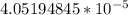`4.05194845*10^{-5` T