Question

A rectangular box with a square base is to be constructed from material that costs $9 per ft2 for the bottom, $4 per ft2 for the top, and $3 per ft2 for the sides. Find the box of greatest volume that can be constructed for $193. Round your answer to 2 decimals.

Answer 1

V = 23.85 ft³

Explanation:

The dimension of the square base = x ft by x ft

Height of box = y

Volume of the box,
`V = x^(2) y`

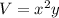
Cost of top = $4 *
`x^(2)`

Cost of the bottom = $9 *
`x^(2)`

Cost of the sides = $3 * 4xy

Total cost = 4x² + 9x² + 12xy

Total cost = 13x² + 12xy

Total cost = $193

193 = 13x² + 12xy

`y = (193 - 13x^(2) )/(12x)`

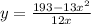
But volume, V = x²y

V =
`(x^(2) (193 - 13x^(2)) )/(12x)`

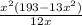
V =
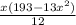`(x (193 - 13x^(2)) )/(12)`...................(1)

At maximum value, V' = 0

0 =
`(193 - 39x^(2) )/(12)`

`39x^(2) = 193\\x^(2) = (193)/(39)`

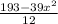
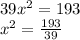
x = 2.23

Put the value of x into (1)

`V = (2.23 (193 - 13*2.23^(2)) )/(12)`

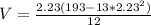
V = 23.85 ft³