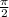Answer with Step-by-step explanation:
We are given that
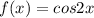
[
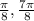 ]
]
1.Cos2x is continuous on given interval [
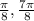 ]
]
2.Cos 2x is differentiable in (
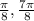 )
)
3.
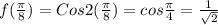
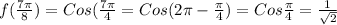
Using the formula
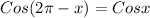
Therefore, f(a)=f(b)
Hence,Cos 2x satisfies the three hypothesis of Roll's theorem on the given interval.

Substitute x=c
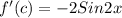

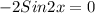
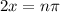
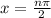
Where
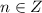
Substitute n=1
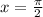 lies in the given interval.
lies in the given interval.
Hence, the value of c=