Question

Use the exponential decay​ model, Upper A equals Upper A 0 e Superscript kt​, to solve the following. The​ half-life of a certain substance is 25 years. How long will it take for a sample of this substance to decay to 60​% of its original​ amount?

Answer 1

18.42 years.

Explanation:

We have been that the half-life of a certain substance is 25 years. We are asked to find time taken by substance to decay to 60​% of its original​ amount.

We will use formula
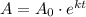`A=A_0\cdot e^(kt)` to solve our problem.

First of all, we will find value of k using
`A=(1)/(2)`,
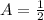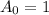`A_0=1` and
`t=25`.

`(1)/(2)=1\cdot e^(k\cdot 25)`

`0.5=e^(25k)`

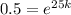
Now we will take natural log of both sides of equation.

`\text{ln}(0.5)=\text{ln}(e^(25k))`

`\text{ln}(0.5)=25k\text{ln}(e)`

`\text{ln}(0.5)=25k(1)`

`k=\frac{\text{ln}(0.5)}{25}`

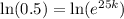
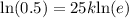
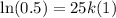
Our function would be
`A=A_0\cdot e^{\frac{\text{ln}(0.5)}{25}t}`.

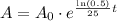Now we have
`A=0.60` and
`A_0=1`.

`0.60=1\cdot e^{\frac{\text{ln}(0.5)}{25}t}`

`0.60=e^{(-0.6931471805599)/(25)t}`

`0.60=e^(-0.02772588722239t)`

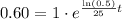
Now we will take natural log on both sides.

`\text{ln}(0.60)=\text{ln}(e^(-0.02772588722239t))`

`\text{ln}(e^(-0.02772588722239t))=\text{ln}(0.60)`

`-0.02772588722239t\cdot \text{ln}(e)=\text{ln}(0.60)`

`-0.02772588722239t\cdot 1=\text{ln}(0.60)`

`(-0.02772588722239t)/(-0.02772588722239)=\frac{\text{ln}(0.60)}{-0.02772588722239}`

`t=(-0.5108256237659907)/(-0.02772588722239)`

`t=18.424139854`

`t\approx 18.42`

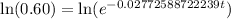
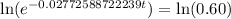
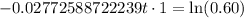
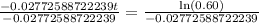
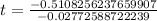
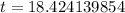
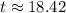
Therefore, it will take approximately 18.42 years for a sample of this substance to decay to 60​% of its original​ amount