Question

A 30-kg child stands at one end of a floating 20-kg canoe that is 5.0-m long and initially at rest in the water. The child then slowly walks to the other end of the canoe. How far does the canoe move in the water, assuming water friction is negligible

Answer 1

The canoe move 3 m in water.

Step-by-step explanation:

Given that,

Mass of the child, m = 30 kg

Mass of canoe, M = 20 kg

Length of canoe, L = 5 m

• Since initially the boat is floating, its center of mass was at rest. So, when child moves on the boat from one end to the other end, the boat moves in opposite direction in such a way that the displacement of their center of mass remains at rest.
• Let x be the displacement of canoe in opposite direction to the motion of child, therefore displacement of child is L - x

So, the displacement of the center of mass is given by :

`d_(cm)=(m(L-x)-Mx)/(m+M)\\\\0=(m(L-x)-Mx)/(m+M)\\\\m(L-x)-Mx=0\\\\30(5-x)-20x=0\\\\x=3\ m`

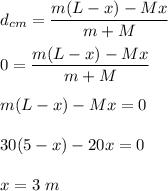
So, the canoe move 3 m in water.