Answer:
0.54704 is the probability that the company will receive atleast 8 calls.
Explanation:
We are given the following information in the question:
Mean number of calls = 8 calls per hour
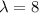
The distribution of calls Hot Line receives can be treated as a Poisson distribution.
We have to find the probability that the company will receive at least 8 calls
Formula:
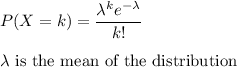
P(atleast 8) =
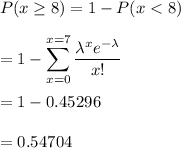
Thus, 0.54704 is the probability that the company will receive atleast 8 calls.