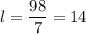Answer:
Length = 14 in, width = 7 in
Explanation:
The area of the page
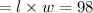
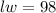
The length of the printable area is gotten by subtracting the top and bottom margins from the length of the page
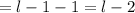
The width of the printable area is gotten by subtracting the left and right margins from the width of the page
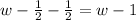
The area of the printable area is
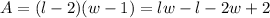
But
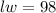 ,
,
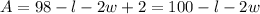
Also, from
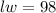 ,
,
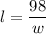
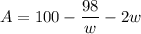
To maximize this area,
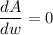
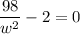
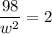
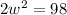
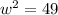
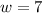
Hence,