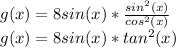Question

The rate of change of the function f(x) = 8 sec(x) + 8 cos(x) is given by the expression 8 sec(x) tan(x) − 8 sin(x). Show that this expression can also be written as 8 sin(x) tan2(x). Use the Reciprocal and Pythagorean identities, and then simplify.

Answer 1

`8sec(x)tan(x)-8sin(x)=8sin(x)tan^2(x)`

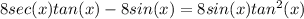
Explanation:

We are going to call g(x) the expression 8 sec(x) tan(X) - 8sin(x), so:

`g(x)=8sec(x)tan(x)-8sin(x)`

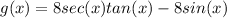
Now, we have the following identities:

1.
`sec(x)=(1)/(cos(x))`

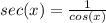
2.
`tan(x)=(sin(x))/(cos(x))`

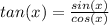
So, if we replace that identities on the initial equation, we have:

`g(x)=(8(1)/(cos(x))*(sin(x))/(cos(x)))-8sin(x)\\g(x)=8(sin(x))/(cos^(2)(x))-8sin(x)`

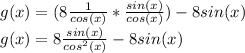
Now, we need to sum both terms in the equation as:

`g(x)=8(sin(x))/(cos^(2)(x))-8sin(x)\\g(x)=(8sin(x)-8sin(x)cos^(2)(x))/(cos^(2)(x))`

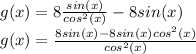
Then, factoring 8sin(x), we get:

`g(x)=8sin(x)*(1-cos^2(x))/(cos^2(x))`

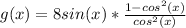
Now, we also have the following identity:

`sin^(2)(x) + cos^2(x)=1\\or\\sin^(2)(x) = 1-cos^(2)(x)`

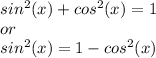
Finally, replacing on g(x), we get:

`g(x)=8sin(x)*(sin^2(x))/(cos^2(x))\\g(x)=8sin(x)*tan^2(x)`

Answer 2

Shown - See explanation

Explanation:

Solution:-

- The given form for rate of change is:

8 sec(x) tan(x) − 8 sin(x).

- The form we need to show:

8 sin(x) tan2(x)

- We will first use reciprocal identities:

`8(sin(x))/(cos^2(x)) - 8sin(x)`

- Now take LCM:

`8(sin(x)- sin(x)*cos^2(x))/(cos^2(x))`

- Using pythagorean identity , sin^2(x) + cos^2(x) = 1:

`8*sin(x)*(1- cos^2(x))/(cos^2(x)) = 8*sin(x)*(sin^2(x))/(cos^2(x))`

- Again use pythagorean identity tan(x) = sin(x) / cos(x):

`8*sin(x)*tan^2(x)`