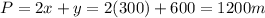Answer:
1200 m
Explanation:
We are given that
Area of pasture,A=180000 square meter
We have to find the least amount of fencing required to enclose such a pasture.
Let length of pasture,=x
Width of pasture,b=y
Area of pasture=
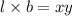
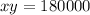
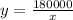
Fencing required=2x+y
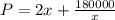
Differentiate w.r.t x
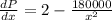
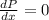
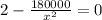
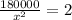
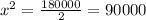
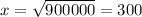 m
m
It is always positive because length cannot be negative.
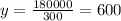 m
m
Again differentiate w.r.t x
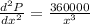
Substitute x=300
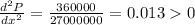
The fence is minimum at x=300
Therefore, fencing required to enclose such a pasture