Question

Consider an object that at one time has energy E1 and momentum p1 and at a later time has energy E2 and momentum p2. Use the relativistic energy-momentum equation E2=p2c2+m2c4 to find the value of E22−E21.

Answer 1

Complete Question

Consider an object that at one time has energy E_1 and momentum p 1 and at a later time has energy E_2 and momentum p_2 . Use the relativistic energy-momentum equation E 2 = p 2 c 2 + m 2 c 4 to find the value of

E 2 2 − E 2 1 . Express your answer in terms of p_1 , p_2 , m and c

Answer:

The value of
`E_2^2 -E_1^2`
`=(p_2^2 -p_1^2)c^2`

Step-by-step explanation:

The objective of the Question is to obtain

`E_2^2 -E_1^2`

Energy momentum equation is mathematically represented as

`E^2 = p_1 c^2 +m^2 c^2`

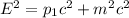
Where c is velocity and m is mass

From the question we are told that

`E_2^2 = p_2c^2 +m^2c^2`

Therefore

`E^2_1 = p_1c^2 +m^2c^2`

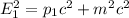
Now

`E_2^2 -E_1^2`
`=(p_2^2 -p_1^2)c^2`