Question

Certain neutron stars (extremely dense stars) are believed to be rotating at about 0.70 rev/s. If such a star has a radius of 19 km, what must be its minimum mass so that material on its surface remains in place during the rapid rotation

Answer 1

The minimum mass so that material on its surface remains in place during the rapid rotation is
`5.03* 10^(22)\ kg`.

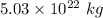Step-by-step explanation:

Given that,

Certain neutron stars are believed to be rotating at about 0.70 rev/s.

Radius of the star, r = 119 km

When the star rotates the gravitational force is balanced by the centripetal force as :

`G(Mm)/(r^2)=m\omega^2 r\\\\M=(\omega^2r^3)/(G)\\\\M=((0.7)^2* (19000)^3)/(6.67* 10^(-11))\\\\M=5.03* 10^(22)\ kg`

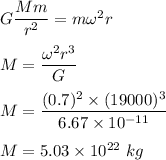
So, the minimum mass so that material on its surface remains in place during the rapid rotation is
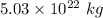`5.03* 10^(22)\ kg`.