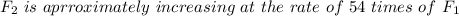Answer:
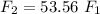
Step-by-step explanation:
Given that:
A tugboat tows a ship with a constant force of magnitude F1 and then increases the ship's speed during a 10 s interval with 2.0 km/h.
If F = ma
we can say for
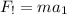
where :
 since F is constant so ; acceleration too is constant
since F is constant so ; acceleration too is constant
 = 2.0 km/h
= 2.0 km/h
=
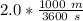
= 0.556 m/s

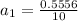
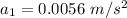
Similarly ;
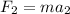
We can as well say ;
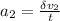

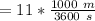
= 3.0556 m/s²
Now; the additional force acting on the ship in the same direction of the force i.e the net force is :
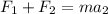
Thus; we can say:
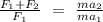
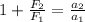
![F_2 = [(a_2)/(a_1)-1 ]F_1](https://img.qammunity.org/2021/formulas/physics/college/ucdvhmhpj6oxb5frpm7neq7mz7pbty4igg.png)
![F_2 = [ (0.30556 \ m/^2)/(0.0056 \ m/s^2) - 1 ] F_1](https://img.qammunity.org/2021/formulas/physics/college/xbyfjs01g0p6eyyabifm3don1fzzpc79f3.png)
![F_2 = [ (0.30556 \ m/^2 - 0.0056 \ m/s ^2)/(0.0056 \ m/s^2)] F_1](https://img.qammunity.org/2021/formulas/physics/college/6jrznadgeytjd3fhsqt649xbgrgid3ec0t.png)
![F_2 = [ (0.29996 \ m/s ^2)/(0.0056 \ m/s^2)] F_1](https://img.qammunity.org/2021/formulas/physics/college/7pjs0sp95uo2ur0kj909sxxbn1o9jt9sni.png)
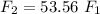
Thus, the magnitude of F1 and F2 compare in a way that says: