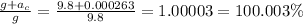Answer:
a. 0.0628 m
b. 0.000263 m/s2
c.99.997%
d.100.003%
Step-by-step explanation:
Suppose the radius is 15 m and each loop takes 25 minutes (25*60 = 1500 seconds) to complete. The circumference of the Ferris wheel would be
C = 2πR = 2π*15 = 94.25 m
The your speed is the length of each loop per unit of time to complete each loop
v = C/t = 94.25 / 1500 = 0.0628 m/s
b. Since the circular motion is constant, the only acceleration from the motion is the centripetal acceleration, which can be calculated as the following:
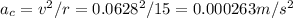
c. Let g = 9.8 m/s^2. At top of the ride, the centripetal acceleration would be pushing you up, while gravity pushes you down, so the weight you experience (compare to standing on ground would be):

d. At the bottom of the ride, both centripetal acceleration and gravity would be pushing you downward, making you feel like