Answer:
The probability that the sample proportion will be less than 0.11 = .9982
Explanation:
Given -
Suppose the true proportion is 0.07 .
true proportion
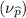 = p = 0.07
= p = 0.07
q = 1 - p = 1 - 0.07 = 0.93
n = 343
Standard deviation
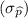 =
=
 =
=
 = .0137
= .0137
the probability that the sample proportion will be less than 0.11 =
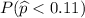 =
=
 using[
using[
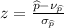 ]
]
=

= .9982