Answer:
The final velocity of the thrower is
 and the final velocity of the catcher is
and the final velocity of the catcher is
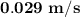 .
.
Step-by-step explanation:
Given:
The mass of the thrower,
 .
.
The mass of the catcher,
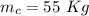 .
.
The mass of the ball,
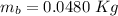 .
.
Initial velocity of the thrower,
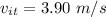
Final velocity of the ball,
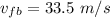
Initial velocity of the catcher,
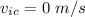
Consider that the final velocity of the thrower is
 . From the conservation of momentum,
. From the conservation of momentum,
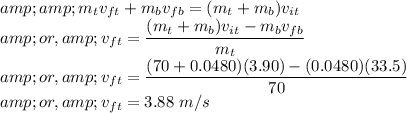
Consider that the final velocity of the catcher is
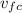 . From the conservation of momentum,
. From the conservation of momentum,
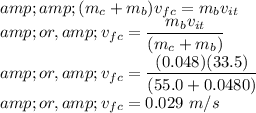
Thus, the final velocity of thrower is
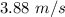 and that for the catcher is
and that for the catcher is
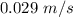 .
.