Answer:
The strength of magnetic field is 0.25 T
Step-by-step explanation:
Time period
 sec
sec
Mass of proton
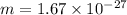 kg
kg
Charge of proton
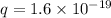 C
C
Here proton moves in circular path
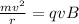
Velocity of proton is given by,
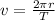
Put the value of velocity in above equation,

Now magnetic field is given by,
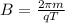
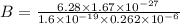
 T
T
Therefore, the strength of magnetic field is 0.25 T