Question

Two methods, A and B, are available for teaching a certain industrial skill. The failure rate is 35\% for A and 15\% for B. However, B is more expensive There hence is used only 40\% of the time, while A is used 60\% of the time. A worker is taught the skill by one of the methods but fails to learn it correctly. What is the probability that he was taught by method A?

Answer 1

Therefore the probability that he was taught by method A is 0.78.

Step-by-step explanation:

Probability:

The ratio of the number of favorable outcomes to the number of all possible outcomes.

Bayes' Rule:

If the events
`B_1`,
`B_2`, .....
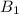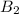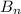`B_n` from a portion of a sample space S and A is any events of A, then

`P(B_i|A)=(P(B_i)P(A|B_i))/(\sum_(j=1)^kP(B_j)P(A|B_j))`

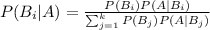
Given that,

There are two available method for teaching A and B.

The failure rate for A is 35%

That is P(F|A) =35%=0.35

The failure rate for B is 15%

That is P(F|A) =15%=0.15

A used 40% of the time.

P(A)=40%=0.40

B used 60% of the time.

P(A)=60%=0.60

To find P(A|F) , we use the Bayes's rule.

`P(A|F)=(P(A)P(F|A))/(P(A)P(F|A)+P(B)P(F|B))`

`=(0.60* 0.35)/(0.60* 0.35+0.40* 0.15)`

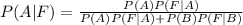
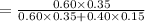
=0.78

Therefore the probability that he was taught by method A is 0.78.