Answer:
0.63
Step-by-step explanation:
We are given that
Radius of earth,
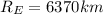
Radius of orbit A,
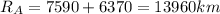
Radius of orbit B,
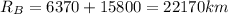
We have to find the ratio of the potential energy of satellite B to that of satellite A in orbit.
Potential energy of orbit A=
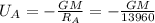
Potential energy of orbit B=
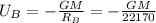
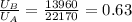
Hence,the ratio of the potential energy of satellite B to that of satellite A in orbit=0.63