Answer:
(a) 81000 V, (b) 40500 V, (c) 0 V
Step-by-step explanation:
Given:
side of square, a = 4 m
charge on each corner , q = + 9 micro coulomb
The formula for the potential is
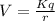
where, k is the Coulombic constant.
(a)
All the charges are positive:
Let V1, V2, V3 and V4 be the potential at the centre O due to the charges at 1, 2,3 and 4.
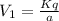
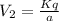
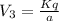
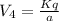
Total potential at the centre of square is
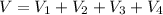

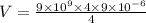
V = 81000 V
(b)
Three charge are positive and one is negative
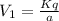
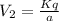
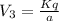
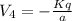
Total potential at the centre of the square is
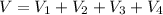
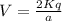
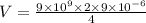
V = 40500 V
(c)
two charge are positive and the other two are negative
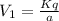
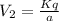
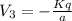
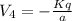
Total potential at the centre of the square is
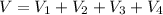
V = 0 V