Question

The average score of all golfers for a particular course has a mean of 64 and a standard deviation of 3. Suppose 36 golfers played the course today. Find the probability that the average score of the 36 golfers exceeded 65. Round to four decimal places.

Answer 1

the probability that the exceeded 65 = 0.3707

The average score of the 36 golfers exceeded 65

= 36 X 0.3707 = 13.3452

Explanation:

Step 1:-

The average score of all golfers for a particular course has a mean of 64 and a standard deviation of 3.

mean (μ) = 64

standard deviation (σ) =3

by using normal distribution

given (μ) = 64 and (σ) =3

i) when x =65

`z = (x-mean)/(S.D) = (65-64)/(3) = 0.33 >0`

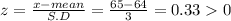
P( X≥ 65) = P(z≥0.33)

= 0.5 - A(z₁)

= 0.5 - 0.1293 (see normal table)

= 0.3707

The average score of the 36 golfers exceeded 65

= 36 X 0.3707 = 13.3452