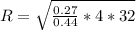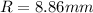Answer:
The radius is
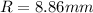
Step-by-step explanation:
Generally Magnetic field due to a current carrying wire is is mathematically represented as
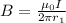
Where
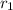 is the distance from the axis of the wire to the first point we are considering
is the distance from the axis of the wire to the first point we are considering
I is the current
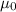 is the permeability of free space
is the permeability of free space
Making I the subject
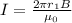
Generally Magnetic field inside a current carrying wire is is mathematically represented as
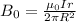
Now the r here is the distance from the axis of the wire to the second point we are considering
And R i the radius of the wire
Making R the subject of the formula
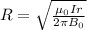
Substituting for I we have
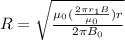
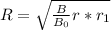
Where B = 0.27mT
And
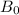 = 0.44mT
= 0.44mT
r = 32mm
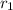 = 4.0mm
= 4.0mm
Substituting values