Question

Suppose you want to determine the resistance of a resistor that is nominally 100 . You should be able to apply 10 V across the resistor and measure about 100 mA. Since there are variations in your resistor values, the resistor you chose is not exactly 100 . First, you measure y1 = 102 mA. Then, you ask a friend to measure, and she gets y2 = 97 mA. a. What do you get for the resistance value if you use the two measurements separately (two values)? b. Set it up as a linear system with measurement y = [y1y2]T and a single resistance value x.

Answer 1

a) For y = 102 mA, R = 98.039 ohms

For y = 97 mA, R = 103.09 ohms

b) Check explanatios for b

Step-by-step explanation:

Applied voltage, V = 10 V

For the first measurement, current
`y_(1) = 102 mA = 0.102 A`

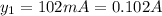
According to ohm's law, V = IR

R = V/I

Here,
`I = y_(1)`

`R = (V)/(y_(1) ) \\R = (10)/(0.102) \\R = 98.039 ohms`

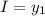
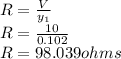
For the second measurement, current
`y_(2) = 97 mA = 0.097 A`

`R = (V)/(y_(2) )`

`R = (10)/(0.097) \\R = 103 .09 ohms`

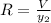
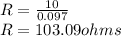
b)
`y = \left[\begin{array}{ccc}y_(1) &y_(2) \end{array}\right] ^(T)`

`y = \left[\begin{array}{ccc}y_(1) \\y_(2) \end{array}\right]`

`y = \left[\begin{array}{ccc}102*10^(-3) \\97*10^(-3) \end{array}\right]`

A linear equation is of the form y = Gx

The nominal value of the resistance = 100 ohms

`x = \left[\begin{array}{ccc}100\end{array}\right]`

`\left[\begin{array}{ccc}102*10^(-3) \\97*10^(-3) \end{array}\right] = \left[\begin{array}{ccc}G_(1) \\G_(2) \end{array}\right] \left[\begin{array}{ccc}100\end{array}\right]\\\left[\begin{array}{ccc}G_(1) \\G_(2) \end{array}\right] = \left[\begin{array}{ccc}102*10^(-5) \\97*10^(-5) \end{array}\right]`