Question

A single slit, 0.10 mm wide is illuminated by a wavelength of light 461.9 nm. An observing screen is 1.0 m away. What is the angular width of the central maximum? {0.53o} A single slit of width 0.1 mm is illuminated by a 600 nm light. How far is the third dark band from the central bright band on a screen 40 cm from the slit? (1.03o, 0.72 cm)

Answer 1

a) Angular width of the central maximum = 0.5294°

b) The distance of the third dark band from the central bright band = 0.72 cm

Step-by-step explanation:

a) Width of the slit, d = 0.1 mm = 0.0001 m

Wavelength of the light,
`\lambda = 461.9 nm = 461.9 * 10^(-9) m`

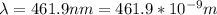
The distance of the screen, R = 1 m

`d sin \theta = \lambda`

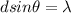
where
`\theta` is the angle at which first minima is visible

`0.0001 sin \theta = 461.9 * 10^(-9) \\sin \theta =(461.9 * 10^(-9))/(0.0001) \\sin \theta = 0.004619\\\theta = sin^(-1) 0.004619\\\theta = 0.2647^(0)`

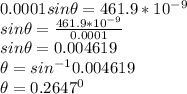
The angular width of the central maximum =
`2 \theta`

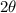
Angular width of the central maximum = 2 * 0.2647

Angular width of the central maximum = 0.5294°

b) d = 0.1 mm = 0.0001 m

`\lambda = 600 nm = 600 * 10^(-9) m`

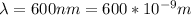
R = 40 cm = 0.4 m

The distance from central bright band to third dark band, is given by the formula:

`y = (3 \lambda R)/(d) \\y = (3 * 600 * 10^(-9)*0.4 )/(0.0001) \\y = 0.0072 m`

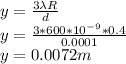
y = 0.72 cm