Question

Squares with sides of length x are cut out of each corner of a rectangular piece of cardboard measuring 13 ft by 8 ft. The resulting piece of cardboard is then folded into a box without a lid. Find the volume of the largest box that can be formed in this way.

Answer 1

length of box = 13 - 2 (1.61) = 9.78 ft

width = 8 - 2(1.61) = 4.78 ft

height, x = .61 ft

Explanation:

Length of sheet, L = 13 ft

width of sheet, W = 8 ft

height of the box, h = x

So, after cutting the sides, the length of the box is (13 -2x) and the width is (8 - 2x) and height is x.

Volume of the box = length x width x height

V = (13 - 2x)(8 - 2x) x

V = 4x³ - 42x² + 104 x

Differentiate with respect to x.

dV/dx = 12x² - 84 x + 104

Put it equal to zero for maxima and minima:

12x² - 84 x + 104 = 0

3x² - 21 x + 26 = 0

`x=(21\pm √(441-312))/(6)`

`x=(21\pm 11.36)/(6)`

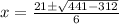
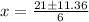
x = 5.4 ft or 1.61 ft

`(d^(2)V)/(dx^(2))=24x - 84`

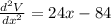
for x = 5.4, d²V/dx² = 24(5.4) - 84 = + 45.6

for x = 1.61 , d²V/dx² = 24(1.61) - 84 = - 45.4

So, for x = 1.61 the volume is maximum.

length of box = 13 - 2 (1.61) = 9.78 ft

width = 8 - 2(1.61) = 4.78 ft

height, x = .61 ft