Corrected Question:
Three resistors with values of 5.0 ohm, 10 ohm, and 15 ohms and are connected in series in a circuit with a 9.0-V battery. (a) What is the total equivalent resistance? (b) What is the current in each resistor? (c) At what rate is energy delivered to the 15 ohm resistor?
Answer:
(a) 30 ohm
(b) 0.3A
(c) 1.35W
Step-by-step explanation:
(a) When resistors are connected in series, their total equivalent resistance is the sum of their individual resistances. Therefore, the total resistance, R, of the resistors in question is;
R = 5.0 + 10 + 15
R = 30 ohm
Therefore, the total equivalent resistance is 30 ohm
(b) Also, when resistors are connected in series, the same current passes through them and the value of the current is equal to the ratio of the voltage across their combined (total) resistance to their total resistance. Therefore, to get the current, I, through each resistor, we find the ratio of the voltage, V, across their combined resistance to their total resistance, R as follows;
I =
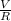------------------(i)
From the question;
V = 9.0V
R = 30 ohm (as calculated above)
Substitute these values into equation (i) as follows;
I =
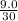
I = 0.3A
Therefore the current in each resistor is 0.3A
(c) The rate at which energy is delivered to the 15 ohm resistor is the measure of the power, P, supplied to the resistor and is given by;
P = I²R --------------------(ii)
Where;
R = the value of the resistor = 15 ohm
I = current in the resistor = 0.3A
Substitute the values into equation (ii) as follows;
P = (0.3)² x 15
P = 0.09 x 15
P = 1.35W
Therefore, the rate at which energy is delivered to the 15 ohm resistor is 1.35W