Answer:
a)
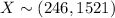
b) 0.1191
c)
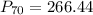
Explanation:
We are given the following information in the question:
Mean, μ = 246 feet
Standard Deviation, σ = 39 feet
We are given that the distribution of distance of fly balls is a bell shaped distribution that is a normal distribution.
a) Distribution of X
Let X be the distance in feet for a fly ball. Then,
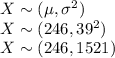
b) Probability that a randomly hit fly ball travels less than 200 feet.
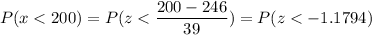
Calculation the value from standard normal z table, we have,
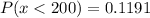
c) 70th percentile for the distribution of fly balls.
We have to find the value of x such that the probability is 0.7
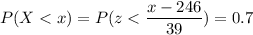
Calculation the value from standard normal z table, we have,
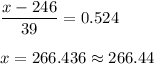
The 70th percentile for the distribution of fly ball is 266.44 feet.