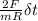Answer:
the angular velocity of the carousel after the child has started running =
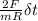
Step-by-step explanation:
Given that
the mass of the child = m
The radius of the disc = R
moment of inertia I =
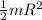
change in time =
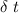
By using the torque around the inertia ; we have:
T = I×∝
where
R×F = I × ∝
R×F =
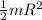 ∝
∝
F =
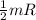 ∝
∝
∝ =
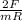 ( expression for angular angular acceleration)
( expression for angular angular acceleration)
The first equation of motion of rotating wheel can be expressed as :
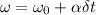
where ;
∝ =
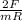
Then;
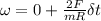
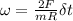
∴ the angular velocity of the carousel after the child has started running =