Question

Assuming that the smallest measurable wavelength in an experiment is 0.950 fm , what is the maximum mass of an object traveling at 241 m ⋅ s − 1 for which the de Broglie wavelength is observable?

Answer 1

0.0289 x 10⁻¹⁹kg

Step-by-step explanation:

The de Broglie wavelength, λ, of a particle varies inversely with the momentum (the product of the mass, m, and velocity, v) of the particle. i.e

λ ∝
`(1)/(mv)`

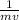
λ =
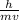`(h)/(mv)` ------------------------(i)

Where;

h = constant of proportionality called Planck's constant = 6.626 x 10⁻³⁴Js

From the question;

λ = 0.950fm = 0.950 x 10⁻¹⁵m

v = 241ms⁻¹

Substitute these values into equation (i) as follows;

0.950 x 10⁻¹⁵ =
`(6.626 * 10^(-34))/(m*241)`

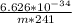
Solve for m;

m =
`(6.626 * 10^(-34))/(0.950*10^(-15) * 241)`

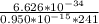
m = 0.0289 x 10⁻¹⁹kg

Therefore, the maximum mass of the object is 0.0289 x 10⁻¹⁹kg

Answer 2

The maximum mass is
`2.89x10^(-21)Kg`

Step-by-step explanation:

The wavelength of the electron can be determined by means of the De Broglie equation.

`\lambda = (h)/(p)` (1)

Where h is the Planck's constant and p is the momentum.

`\lambda = (h)/(mv)`

`m = (h)/(\lambda v)` (2)

Where m is the mass and v is the velocity.

Before using equation 2 it is necessary to express the wavelength from femtometers to meters.

`\lambda = 0.950fm .(1m)/(1x10^(15)fm)` --
`9.5x10^(-16)m`

Finally, equation 2 can be used.

`m = (6.624x10^(-34) J.s)/((9.5x10^(-16)m)(241m/s))`

But
`1J = Kg.m^(2)/s^(2)`

`m = (6.624x10^(-34) Kg.m^(2)/s^(2).s)/((9.5x10^(-16)m)(241m/s))`

`m = 2.89x10^(-21)Kg`

Hence, the maximum mass is
`2.89x10^(-21)Kg`