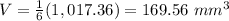Answer:
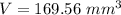
Explanation:
we know that
The volume of the cone is given by te formula
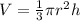
we have
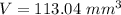
substitute
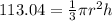
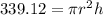 ----> equation A
----> equation A
Remember that
A sphere has the same height and a circular base with the same diameter
That means----> The diameter of the sphere is equal to the height of the cone and the radius of the sphere is equal to the radius of the base of cone
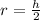
equation A is equal to
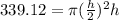
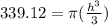
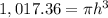 -----> equation B
-----> equation B
The volume of the sphere is given by
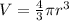
substitute
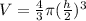
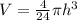
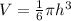
substitute equation B in the expression above