Question

Point c has the coordinates (-1,4) and point D has coordinates (2,0).

What it the distance between points C and D

Answer 1

Given:

The coordinates of the point C is (-1,4) and the coordinates of the point D is (2,0).

We need to determine the distance between the points C and D

Distance between C and D:

The distance between the two points can be determined using the formula,

`d=\sqrt{\left(x_(2)-x_(1)\right)^(2)+\left(y_(2)-y_(1)\right)^(2)}`

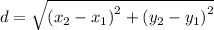
Let us substitute the coordinate (-1,4) and (2,0) for the coordinates
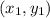`(x_1,y_1)` and
`(x_2,y_2)`

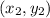
Thus, we have;

`d=\sqrt{\left(2+1\right)^(2)+\left(0-4\right)^(2)}`

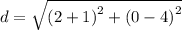
Simplifying, we get;

`d=\sqrt{\left(3\right)^(2)+\left(-4\right)^(2)}`

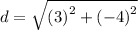
Squaring the terms, we have;

`d=√(9+16)`

`d=√(25)`

`d=5`

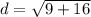
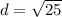
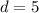
Thus, the distance between the points C and D is 5 units.