Question

What is
`(√(-3) )^4`

Answer 1

9

Explanation:

I am guessing you´re simplifying this equation.

(The 4 is still an exponent)

Rewrite
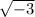`√(-3)` as
`√(-1(3))`

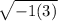
Now rewrite the equation before as
`(√(-1) *√(3) )^(4)`

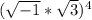
Now rewrite
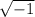`√(-1)` as
`i`

`(i*√(3) )^(4)`

You will then apply the product rule to
`i√(3)`

`i^(4) √(3) ^(4)`

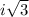
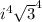
Now rewrite
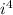`i^(4)` as 1

You first have to rewrite

`i^(4) as (i^(2) )^(2) .`

`(i^(2) )^(2) √(3) ^(4)`

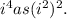
Now
`i^(2) as -1`

`(-1)^(2) √(3) ^(4)`

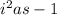
Then raise -1 to the second power

`1√(3) ^(4)`

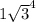
Now multiply
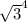`√(3) ^(4)` by
`1`

`√(3) ^(4)`

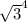
Now here comes the longest part

Rewrite
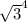`√(3) ^(4)` as
`3^(2)`

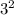
You first have to use
`\sqrt[n]{a^(x) } = a^{(x)/(n) }` to rewrite
`√(3)` as
`3^{(1)/(2) }`

`(3^{(1)/(2) } )^(4)`

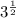
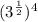
Apply the power rule and multiply the exponents ,
`(a^(m) )^(n) = a^(mn)`

`3^{(1)/(2) } *4`

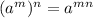
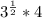
Now combine
`(1)/(2)` and
`4`

`3^{(4)/(2) }`

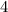
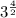
Now you have cancel the common factor of 4 and 2

Factor 2 out of 4

`3^{(2*2)/(2) }`

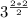
Cancel the common factors

Now factor 2 out of 2

`3^{(2*2)/(2(1)) }`

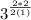
Cancel the common factor

`3^{(2*2)/(2*1) }`

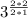
Rewrite the expression

`3^{(2)/(1) }`

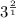
Divide 2 by 1

`3^(2)`

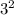
Raise 3 to the second power´

9

Answer 2

9

Explanation: