Question

Agan Interior Design provides home and office decorating assistance to its customers. In normal operation, an average of 2.5 customers arrive each hour. One design consultant is available to answer questions and make product recommendations. The consultant averages 10 minutres with each customer.

A. Compute the operating characteristics of the customers wiating line, assuming posson arrivals and exponential service times.

B. Service goals dictate that an arriving customer should not wait for service more than an average of 5 minutes. Is this gaol being met?

C. If the consultant can reduce the average time spent per customer to 8 minutes, what is the mean service rate? Will the service goal be met?

Answer 1

A) Single-server single-phase model (M/M/1).

`\lambda=2.5 \,customers/hour\\\\\mu=6\,customers/hour`

B) The goal is not met, as the average time waiting for service is 5.56 minutes.

C) The new mean service rate is 7.5 customers/hour.

In this case, the average time waiting for service is 4 minutes, so the goal is met.

Step-by-step explanation:

A) This situation can be modeled as a single-server single-phase model (M/M/1).

The mean arrival rate is 2.5 customers per hour.

`\lambda=2.5 \,customer/h`

The mean service rate is 6 customers per hour, calculated as:

`\mu=(60\, min/h)/(10 \,min/customer)=6\, customer/h`

B) The average waiting time for a customer can be expressed as:

`W_q=(\lambda)/(\mu)(1)/(\mu-\lambda) =(2.5)/(6)(1)/(6-2.5) =0.417*0.222=0.093\,hours\\\\W_q=0.093\,hours*(60min/h)=5.56 \,min`

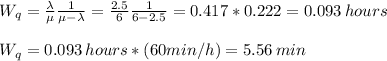
The average waiting time is 5.56 minutes, so it is more than the goal of 5 minutes.

C) If the average time spent per customer to 8 minutes, the mean service rate becomes

`\mu=(60\, min/h)/(8 \,min/customer)=7.5\, customer/h`

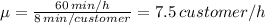
An the average waiting time for the service now becomes:

`W_q=(\lambda)/(\mu)(1)/(\mu-\lambda) =(2.5)/(7.5)(1)/(7.5-2.5) =0.333*0.2=0.067\,hours\\\\W_q=0.067\,hours*(60min/h)=4 \,min`

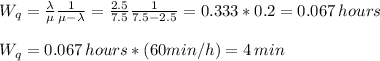
The average time is now 4 minutes, so the goal is achieved.