Answer:
a) E =0, b) E = 1,129 10¹⁰ N / C , c) E = 3.33 10¹⁰ N / C
Step-by-step explanation:
To solve this exercise we can use Gauss's law
Ф = ∫ E. dA =
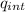 / ε₀
/ ε₀
Where we must define a Gaussian surface that is this case is a sphere; the electric field lines are radial and parallel to the radii of the spheres, so the scalar product is reduced to the algebraic product.
E A =
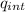 /ε₀
/ε₀
The area of a sphere is
A = 4π r²
E = q_{int} / 4πε₀ r²
k = 1 / 4πε₀
E = k q_{int} / r²
To find the charge inside the surface we can use the concept of density
ρ = q_{int} / V ’
q_{int} = ρ V ’
V ’= 4/3 π r’³
Where V ’is the volume of the sphere inside the Gaussian surface
Let's apply this expression to our problem
a) The electric field in center r = 0
Since there is no charge inside, the field must be zero
E = 0
b) for the radius of r = 6.0 cm
In this case the charge inside corresponds to the inner sphere
q_{int} = 5.0 4/3 π 0.06³
q_{int} = 4.52 10⁻³ C
E = 8.99 10⁹ 4.52 10⁻³ / 0.06²
E = 1,129 10¹⁰ N / C
c) The electric field for r = 12 cm = 0.12 m
In this case the two spheres have the charge inside the Gaussian surface, for which we must calculate the net charge.
The charge of the inner sphere is q₁ = - 4.52 10⁻³ C
The charge for the outermost sphere is
q₂ = ρ 4/3 π r₂³
q₂ = 8.0 4/3 π 0.12³
q₂ = 5.79 10⁻² C
The net charge is
q_{int} = q₁ + q₂
q_{int} = -4.52 10⁻³ + 5.79 10⁻²
q_{int} = 0.05338 C
The electric field is
E = 8.99 10⁹ 0.05338 / 0.12²
E = 3.33 10¹⁰ N / C