Step-by-step explanation:
Given that,
Mass of the, m = 0.256 kg
Initial peed of the ball, v = 11.8 m/s
The ball is in contact with the wall for t = 0.066 s
(1) The magnitude of the initial momentum of the racquet ball is given by :
p = mv

(2) It is projected at angle of 29 degrees. The ball makes a perfectly elastic collision with the solid, frictionless wall and rebounds at the same angle with respect to the horizontal.
The change in momentum of the racquet ball is given by :
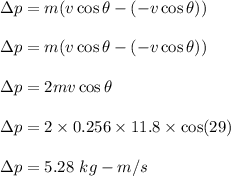
(3) Impulse is equal to the change in momentum.
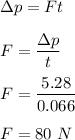
Hence, this is the required solution.