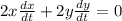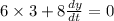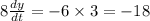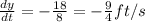Question

A 10 ft long ladder rests against a vertical wall. If the bottom of the ladder slides away from the wall at a rate of 3 ft/s, how fast is the top of the ladder sliding down the wall when the bottom of the ladder is 6 ft from the wall?

Answer 1

`-(9)/(4)ft/s`

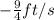
Step-by-step explanation:

We are given that

Length of ladder,z=10ft

Let x be the distance of bottom of ladder from the wall and y be the distance of the top of ladder from the bottom of wall.

`(dx)/(dt)=3ft/s`

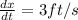
We have to find the rate at which the top of the ladder sliding down the wall when the bottom of the ladder is 6ft from the wall.

i.e.x=6 ft

By Pythagoras theorem

`x^2+y^2=z^2`

`x^2+y^2=(10)^2=100`

`6^2+y^2=(10)^2=100`

`y^2=100-6^2=64`

`y=√(64)=8 ft`

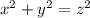
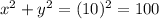
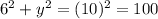
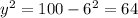
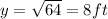
Differentiate w.r.t time

`2x(dx)/(dt)+2y(dy)/(dt)=0`

`6* 3+8(dy)/(dt)=0`

`8(dy)/(dt)=-6* 3=-18`

`(dy)/(dt)=-(18)/(8)=-(9)/(4)ft/s`