Question

If the sum of the first 12 terms of a geometric series is 8190 and the common ratio is 2. Find the first term and the 20th term.

Answer 1

The first term is 2 and the 20th term is 1048576 .

Explanation:

Here we have , If the sum of the first 12 terms of a geometric series is 8190 and the common ratio is 2. We need to Find the first term and the 20th term. Let's find out:

We know that Sum of a GP is :

⇒
`S_n = (a(r^n-1))/(r-1)`

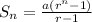
So ,Sum of first 12 terms is :

⇒
`S_1_2 = (a(2^(12)-1))/(2-1)`

⇒
`8190=a(2^(12)-1)`

⇒
`(8190)/(4095)=a`

⇒
`a=2`

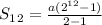
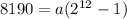
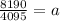
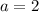
Now , nth term of a GP is

⇒
`a_n = ar^(n-1)`

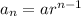
So , 20th term is :

⇒
`a_2_0 = 2(2)^(20-1)`

⇒
`a_2_0 = (2)^(20)`

⇒
`a_2_0 = 1048576`

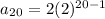
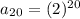
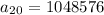
Therefore , the first term is 2 and the 20th term is 1048576 .