Answer:
(A)Therefore the number of dish of three scoops of ice cream is 4,060.
(B)The different kinds of sundaes are 2668.
(C) Therefore total numbers of different sundaes are 25,009,600.
Step-by-step explanation:
- Definition of permutation:
The order of event is counted.
1. Repetition not allowed: P(n,r)
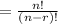
2. Repetition allowed:
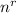
- Definition of combination
The order of event is not counted.
1. Repetition not allowed:
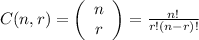
2. Repetition allowed:
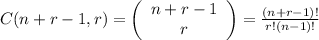
(A)
The order of scope does not matter and repetition allowed. So we use the second formula of combination.
The scoops are then 3 section from 28 different flavors
n=28
r=3
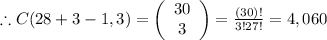
Therefore the number of dish of three scoops of ice cream is 4,060.
(B)
Given a small sundae contains one scoop of ice cream, a sauce and a topping.
The different kinds of sundaes are C(28,1)×C(8,1)×C(12,1)
=28×8×12
=2688
(C)
Scoop:
The order of the scoop does not matter and repetition is allowed.
So, we use the definition of combination of repetition.
n=28
r=3
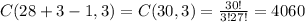
Sauce:
The order of the sauce does not matter and repetition is not allowed.
So, we use the definition of combination of repetition is not allowed.
n=8
r=2
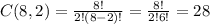
Topping:
The order of the topping does not matter and repetition is not allowed.
So, we use the definition of combination of repetition is not allowed.
n=12
r=3
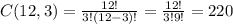
Therefore total number of different sundaes are = (4060×28×220)
=25,009,600