Answer:
a) 166
Explanation:
Explanation:-
Step 1:-
maximum Error of estimation (E) =1.2
we know that maximum Error of estimation
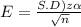
cross multiplication we get ,
E(√n) =σ (zₐ)
Squaring on both sides, we get

Step 2:-
Population of standard deviation σ = 6
level of significance ∝ = 2.576 at 99% of confidence interval
By using formula

substitute all values in above equation
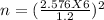
on simplification , we get n = 165.8 ≅166
Conclusion:-
confidence level 99% requires a sample size of at least (n)=166