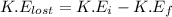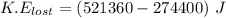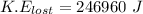Question

1. On the planet Microid, trains that run on air tracks much like the air track you used in lab are the principle means of transportation. A train car with a mass of 6300 kg is traveling at 12.0 m/s when it strikes a second car moving in the same direction at 2.2 m/s. The two stick together and move off with a speed of 4.00 m/s. What is the mass of the second car? Explain your reasoning. (10 pts) 2. How much kinetic energy was lost in the collision? (10 pts)

Answer 1

a) the mass of the second car = 28000 kg

b) the amount of kinetic energy that was lost in the collision =
`246.9*10^3 \ J`

Step-by-step explanation:

Given that:

mass of the train car
`m_1` = 6300 kg

speed of the train car
`v_1` = 12.0 m/s

mass of the second moving car
`m_2` = ???

speed of the second moving car
`v_2` = 2.2 m/s

After strike;

they both move with a speed
`v_f` = 4.00 m/s

a)

Using the conservation of momentum :

`m_1v_1+m_2v_2 = (m_1 + m_2)v_f`

`(6300*12)+m_2(2.2) = (6300 + m_2)4`

`(75600)+m_2(2.2) = 25200 + 4m_2`

`75600 - 25200 = 4m_2 -2.2m_2`

`50400 = 1.8m_2`

`m_2 = (50400)/(1.8)`

`m_2 = 28000 \ kg`

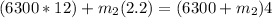
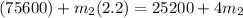
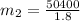
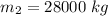
b)

To determine the amount of kinetic energy that was lost in the collision;

we will need to find the difference between the kinetic energy before the collision and after the collision;

i.e

`K.E _(lost) = K.E_(i) - K.E _(f)`

`K.E_(i) = (1)/(2) m_1v_1^2 + (1)/(2)m_2v_2^2`

`K.E_(i) = (1)/(2) (6300)(12)^2 + (1)/(2)(28000)(2.2)^2`

`K.E_(i) = 521360 \ J`

`K.E_(f) = (1)/(2)(m_1 + m_2 ) v_f ^2`

`K.E_(f) = (1)/(2)(6300 + 28000 ) (4)^2`

`K.E_(f) =274400 \ J`

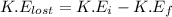
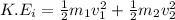
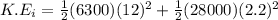
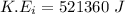
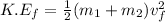
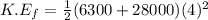
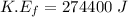
Now; the kinetic energy that was lost in the collision is calculated as follows:

`K.E _(lost) = K.E_(i) - K.E _(f)`

`K.E_(lost) = (521360-274400) \ J`

`K.E_(lost) =246960 \ J`

`K.E_(lost) =246.9 * 10 ^3 \ J`