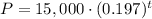Question

Exponential functions

Answer 1

Given:

A population numbers 15,000 organisms initially and grows by 19.7 % each year.

Let P represents the population.

Let t be the number of years of growth.

An exponential model for the population can be written in the form of
`P=a \cdot b^t`

We need to determine the exponential model for the population.

Exponential model:

An exponential model for the population is given by

`P=a \cdot b^t`

where a is the initial value and

and b is the rate of change.

From the given, the value of a is given by

`a=15,000`

Also, the value of b is given by

`b=(19.7)/(100)=0.197`

Thus, substituting the values of a and b in the exponential model, we get;

`P=15,000 \cdot (0.197)^t`

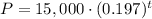
Thus, the exponential model for the given population is
`P=15,000 \cdot (0.197)^t`