Question

Vector u has a magnitude of 3 miles and is directed due east. Vector v has a magnitude

of 3 miles and is directed due north. What are the magnitude and the direction angle for
the resultant vector?

Answer 1

the magnitude and the direction angle for the resultant vector is
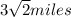`3√(2)miles` and
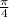`(\pi)/(4)` north east .

Explanation:

Here we have , Vector u has a magnitude of 3 miles and is directed due east. Vector v has a magnitude of 3 miles and is directed due north. We need to find What are the magnitude and the direction angle for the resultant vector. Let's find out:

We know that for two vectors u , v the resultant vector magnitude is given by :

⇒
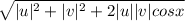`√(|u|^2+|v|^2+2|u||v|cosx)` , where x is angle between two vectors

⇒
`√((3)^2+(3)^2+(3)(3)cos90)`

⇒
`√(9+9+0)`

⇒
`√(18)`

⇒
`3√(2)miles`

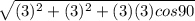
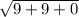
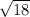
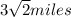
And , direction is given by :

⇒
`Tan^(-1)((|v|)/(|u|))`

⇒
`Tan^(-1)((3)/(3))`

⇒
`Tan^(-1)(1)`

⇒
`(\pi)/(4)`

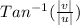
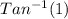
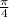
Therefore , the magnitude and the direction angle for the resultant vector is
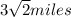`3√(2)miles` and
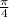`(\pi)/(4)` north east .