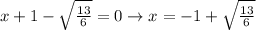Question

What are the zeros of the quadratic function f(x) = 6x2 + 12x – 7? x = –1 – StartRoot StartFraction 13 Over 6 EndFraction EndRoot and x = –1 + StartRoot StartFraction 13 Over 6 EndFraction EndRoot x = –1 – StartFraction 2 Over StartRoot 3 EndRoot EndFraction and x = –1 + StartFraction 2 Over StartRoot 3 EndRoot EndFraction x = –1 – StartRoot StartFraction 7 Over 6 EndFraction EndRoot and x = –1 + StartRoot StartFraction 7 Over 6 EndFraction EndRoot x = –1 – StartFraction 1 Over StartRoot 6 EndRoot EndFraction and x = –1 + StartFraction 1 Over StartRoot 6 EndRoot EndFraction

Answer 1

its A. on edge2021

Explanation:

Answer 2

`x=-1+\sqrt{(13)/(6)}\\x=-1-\sqrt{(13)/(6)}`

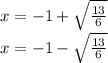
Explanation:

In this problem, the function is

`f(x)=6x^2+12x-7`

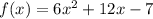
The zeros of the function are the values of x for which the function is zero, so:

`6x^2+12x-7=0`

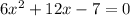
We start by dividing each term by 6:

`x^2+2x-(7)/(6)=0`

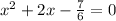
Then we add +1 and -1 to the equation:

`x^2+2x+1-1-(7)/(6)=0`

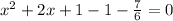
The first 3 terms
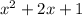`x^2+2x+1` are the square of a binomial,
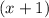`(x+1)`, so this becomes

`(x+1)^2-1-(7)/(6)=0`

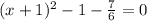
Which is equivalent to

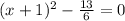`(x+1)^2-(13)/(6)=0` (1)

Now we can use the following rule:

`x^2-a^2 = (x+a)(x-a)`

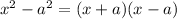
To rewrite (1) as:

`(x+1)^2-(13)/(6)=\\=(x+1+\sqrt{(13)/(6)})(x+1-\sqrt{(13)/(6)})=0`

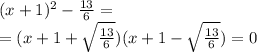
This expression is equal to zero if either one of the two terms in the brackets is equal to zero. Therefore:

1)

`x+1+\sqrt{(13)/(6)}=0 \rightarrow x=-1-\sqrt{(13)/(6)}`

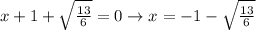
2)

`x+1-\sqrt{(13)/(6)}=0 \rightarrow x=-1+\sqrt{(13)/(6)}`