Question

Find the sum of 46 + 42 + 38 + ... + (-446) + (-450)46+42+38+...+(−446)+(−450)

Answer 1

The sum of the given sequence is -25500.

Explanation:

The given Arithmetic sequence is 46 + 42 +38... +(-446) +(-450).

• The first term of the sequence = 46
• The last term of the sequence = -450
• The common difference ⇒ 42 - 46 = - 4

To find the number of terms in the sequence :

The formula used is
`n = (\frac{a_(n)-a_(1)} {d})+1`

where,

• n is the number of terms.
• 
  `a_(n)` is the late term which is -450.
• 
  `a_(1)` is the first term which is 46.
• d is the common difference which is 4.

Therefore,
`n =((-450-46)/(-4)) +1`

⇒
`n = ((-496)/(-4)) + 1`

⇒
`n = 124 + 1`

⇒
`n =125`

∴ The number of terms, n = 125.

To find the sum of the arithmetic progression :

The formula used is
`S = (n)/(2)(a_(1) + a_(n) )`

where,

• S is the sum of the sequence.
• 
  `a_(1)` is the first term which is 46.
• 
  `a_(n)` is the late term which is -450.

Therefore,
`S = (125)/(2)(46+ (-450))`

⇒
`S = (125)/(2)(-404)`

⇒
`S = 125 * -202`

⇒
`S = -25500`

∴ The sum of the given sequence is -25500.

Answer 2

sum of sequence Find the sum of 46 + 42 + 38 + ... + (-446) + (-450) is -25,250

Explanation:

We need to find sum of sequence : 46 + 42 + 38 + ... + (-446) + (-450)

Given sequence is an AP with following parameters as :

`a=46\\d=42-46=-4`

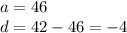
So , Let's calculate how many terms are there as :

⇒
`a_n=a +(n-1)d`

⇒
`-450=46 +(n-1)(-4)`

⇒
`-496=(n-1)(-4)`

⇒
`(-496)/(-4)=n-1`

⇒
`124=n-1`

⇒
`n=125`

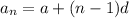
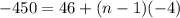
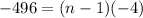
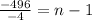
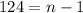
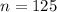
Sum of an AP is :

⇒
`S_n = (n)/(2)(2a+(n-1)d)`

⇒
`S_1_2_5 = (125)/(2)(2(46)+(125-1)(-4))`

⇒
`S_1_2_5 = (125)/(2)(-404)`

⇒
`S_1_2_5 =-25,250`

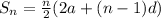
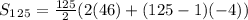
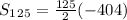
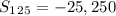
Therefore , sum of sequence Find the sum of 46 + 42 + 38 + ... + (-446) + (-450) is -25,250