Answer:
(a) Mean = 1.6244 (b) Median = 1.65
(c) Mode = 1.35 (d) Range = 1.39
(e) Standard deviation = 0.3325
(f) Variance = 0.1106
(g) Coefficient of variation = 20.47%.
Explanation:
The mean (μ) of a data set is the average value of the data set. The formula to compute mean is:
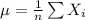
The median (m) is a quantity in statistics that points out where the mid-value of a data set is. In case of, odd number of data-values, the median is given by,
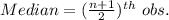
The mode (M) of a data set is the value that appears most often.
The range of a data-set is the difference between the maximum and minimum values in the data-set.
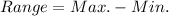
The standard deviation of a data set is a numerical value that represents the amount of variation between the observed values.
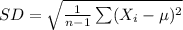
The variance is the square of the standard deviation.

The coefficient of variation (CV) is well defined as the ratio of the standard deviation to the mean. It exhibits the degree of variation in association to the mean of the population.
The formula to compute the coefficient of variation is,
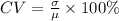
Consider the data set provided.
(a)
Compute the mean as follows:

Thus, the mean of the data is 1.6244.
(b)
Compute the median as follows:
Arrange the data in ascending order as follows:
0.9 , 1.05 , 1.27 , 1.3 , 1.32 , 1.35 , 1.35 , 1.42 , 1.47 , 1.47 , 1.55 , 1.63 , 1.65 ,
1.66 , 1.71 , 1.74 , 1.78 , 1.82 , 1.85 , 1.92 , 1.95 , 1.96 , 2.06 , 2.14 , 2.29

Thus, the median of the data set is 1.65.
(c)
Compute the mode as follows:
Consider the data arranged in ascending order above.
0.9 , 1.05 , 1.27 , 1.3 , 1.32 , 1.35 , 1.35 , 1.42 , 1.47 , 1.47 , 1.55 , 1.63 , 1.65 ,
1.66 , 1.71 , 1.74 , 1.78 , 1.82 , 1.85 , 1.92 , 1.95 , 1.96 , 2.06 , 2.14 , 2.29
The value 1.35 repeats twice and none of the other values repeat themselves.
Thus, the mode of the data set is 1.35.
(d)
Compute the range as follows:
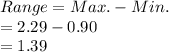
Thus, the range of the data set is 1.39.
(e)
Compute the standard deviation as follows:
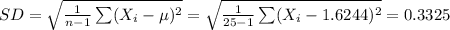
Thus, the standard deviation is 0.3325.
(f)
Compute the variance as follows:
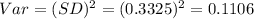
Thus, the variance is 0.1106.
(g)
Compute the coefficient of variation as follows:
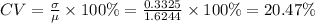
Thus, the coefficient of variation is 20.47%.
The histogram is attached below.