Answer:
(a) The population mean cost per flight is $122.
(b) The probability the sample mean will be within $10 of the population mean cost per flight is 0.9971.
(c) The probability the sample mean will be within $5 of the population mean cost per flight is 0.8638.
Explanation:
Let X = the additional cost charged by the Allegiant Airlines.
The mean additional cost charged per passenger is,
 = $37.
= $37.
The population standard deviation of the additional cost charged per passenger is, σ = $39.
A sample of n = 80 passengers is selected to determine the total cost of their flight on Allegiant Airlines.
(a)
The law of large numbers, in probability concept, states that as we increase the sample size (n), the mean of the sample (
 ) approaches the whole population mean (µ).
) approaches the whole population mean (µ).
That is, as n → ∞,
 → µ.
→ µ.
The sample selected is of size, n = 80. The sample size is quite large.
So the sample mean cost of additional charges can be used to estimate the value of the population mean cost of additional charges.
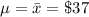
Compute the total cost as follows:
Total cost = Base fare + Mean cost of additional charges
= $85 + $37
= $122
Thus, the population mean cost per flight is $122.
(b)
According to the Central Limit Theorem if we have a population with mean μ and standard deviation σ and we take appropriately huge random samples (n ≥ 30) from the population with replacement, then the distribution of the sample mean will be approximately normally distributed.
Then, the mean of the distribution of sample mean is given by,
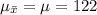
And the standard deviation of the distribution of sample means is given by,
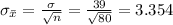
Compute the probability the sample mean will be within $10 of the population mean as follows:
The sample mean be within $10 of the population mean implies:
![[-10\leq (\bar X-\mu_(\bar x))\leq 10]\\=[-10+122\leq \bar X\leq 10+122]\\=[112\leq \bar X\leq 132]](https://img.qammunity.org/2021/formulas/mathematics/college/7dk18nmbquazl4bugzvactx6j6zaf35ff8.png)
Compute the probability as follows:
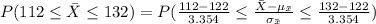
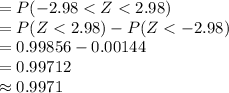
*Use a z-table for the probability.
Thus, the probability the sample mean will be within $10 of the population mean cost per flight is 0.9971.
(c)
Compute the probability the sample mean will be within $5 of the population mean cost per flight as follows:
The sample mean be within $5 of the population mean implies:
![[-5\leq (\bar X-\mu_(\bar x))\leq 5]\\=[-5+122\leq \bar X\leq 5+122]\\=[117\leq \bar X\leq 127]](https://img.qammunity.org/2021/formulas/mathematics/college/z618w2qm28gwwoohroqnailyjpre4sbe1b.png)
Compute the probability as follows:
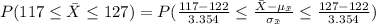
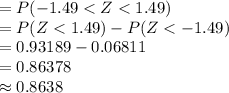
*Use a z-table for the probability.
Thus, the probability the sample mean will be within $5 of the population mean cost per flight is 0.8638.