Answer:
a)
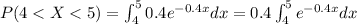

b)
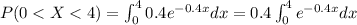
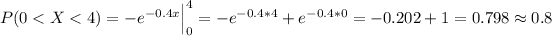
c)

Explanation:
For this case we define the random variable X who represent the duration of a call, in minutes, and the density function for X is given by:
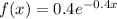
Part a
For this case we want to find this probability:
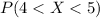
And we can find this probability with this integral:
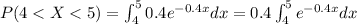

Part b
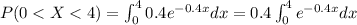
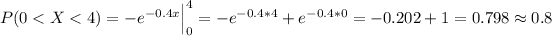
Part c
For this case we want this probability:
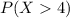
And we can use the complement rule and the result from part b and we got:
