Answer:
The height of the kite is 8.9 feet.
Explanation:
We have drawn diagram for your reference.
Given:
Distance of kite from the line = 12 ft.
According to diagram;
AC = 12 ft
Distance of the shadow of the line taut = 8 ft
According to diagram;
BC = 8 ft
We need to find the height of the kite AB.
Solution:
Let us consider the scenario to be a right angled triangle with right angle at B.
So we will use Pythagoras theorem.
"In a right angle triangle square of sum of 2 sides is equal to square of the third side."
framing in equation form we get;

Substituting the given values we get;
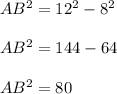
Taking Square root on both side we get;
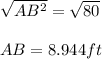
rounding to nearest tenth we get;
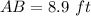
Hence The height of the kite is 8.9 feet.