Question

Consider the right triangle shown.

What is the length of the other leg?
Round your answer to the nearest tenth

Answer 1

Basic Trigonometric Ratios

These are the three basic trigonometric ratios:

• The sine ratio:
  `\sin(\theta)=(opposite)/(hypotenuse)`
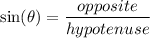
• The cosine ratio:
  `\cos(\theta)=(adjacent)/(hypotenuse)`
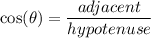
• The rangent ratio:
  `\tan(\theta)=(opposite)/(adjacent)`

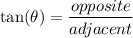
Here, 'opposite' or adjacent are referring to the legs in relation to one of the interior angles of the triangle, θ.

We can use these ratios to help us solve for side lengths or angles, depending on what information is given to us and what information we must solve for.

Solving the Question

We're given:

• The indicated angle (θ) measures 70°
• The adjacent side measures 5.7 units
• We must solve for the other leg, which is the 'opposite' side

Because this question involves the adjacent and the opposite, we can use the tangent ratio to find the answer.

`\tan(\theta)=(opposite)/(adjacent)`

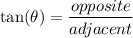
⇒ Plug in the given information:

`\tan(70^\circ)=(opposite)/(5.7)`

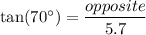
⇒ Multiply both sides by 5.7 to isolate 'opposite:

`5.7\tan(70^\circ)=opposite\\opposite = 15.66062\dots`

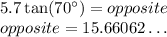
⇒ Round to the nearest tenth:

`opposite=15.7`

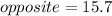
Answer

The length of the other leg is 15.7 units.